[LeetCode刷題筆記] 322 - Coin Change

題目描述：

You are given coins of different denominations and a total amount of money amount. Write a function to compute the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.

You may assume that you have an infinite number of each kind of coin.

Example 1:

Input: coins = [1,2,5], amount = 11
Output: 3
Explanation: 11 = 5 + 5 + 1

Example 2:

Input: coins = [2], amount = 3
Output: -1

Example 3:

Input: coins = [1], amount = 0
Output: 0

Example 4:

Input: coins = [1], amount = 1
Output: 1

Example 5:

Input: coins = [1], amount = 2
Output: 2

Constraints:

1 <= coins.length <= 12
1 <= coins[i] <= 231 - 1
0 <= amount <= 104

一刷題解（Dynamic Programming）：

這題給了我們一個「硬幣幣值」的數組還有一個目標金額，需要我們組合這些硬幣（每枚硬幣都可重複使用），使硬幣總值等同目標金額，每使用一個硬幣，使用次數+1，最後要返回最低的可能使用次數，如果實在是無法湊齊就返回-1。這題看上去思路很簡單，但做起來還是有一點麻煩的。

我對這題的第一反應是使用貪心算法來做，先把硬幣數組進行排序，然後反覆將目標金額減去數組尾部元素（最高幣值），當元素>目標金額，則下標向前。但是這一題並不能這麼做，因為這題的目標是「要不多不少地」湊齊目標金額，也就是說，最快湊齊目標金額的組合有可能不包含最高幣值的硬幣。這樣一來，這題就無法使用貪心算法了。

取而代之，我腦海裡湧現出來的就是DFS，對使用每個硬幣的可能性進行遞歸。每使用一次硬幣，就增加一次步數並把目標金額減去使用硬幣的幣值，然後將這個目標金額向下傳，重複檢查，直到幣值 = 0 或者最小的幣值大於目標金額為止。當然每當一個可能性把步數返回到上一層時，上一層都要判斷這個值是不是這麼多種可能性中的最小值。（if(stepCnt >= 0 && stepCnt < minValue) { minValue = stepCnt + 1; })

最後，把這個結果記錄到作為存儲結果數組的對應索引上，從而省去之後遇到重複問題時的計算時間，這也是Dynamic Programming的核心。

public class Solution {
    public int CoinChange(int[] coins, int amount)
    {
        if (amount == 0) { return 0; }
        Array.Sort(coins);
        int[] memo = new int[amount];
        return ClearCoinPathCounter(coins, amount, memo);
    }
    int ClearCoinPathCounter(int[] coins, int amount, int[] memo)
    {
        //當目標金額=0，找到一種題解
        if (amount == 0) { return 0; }
        //嘗試從存儲結果數組中提取結果，省去下面的計算步驟
        if(memo[amount - 1] != 0) { return memo[amount - 1]; }

        int minValue = int.MaxValue;
        //遍歷硬幣數組的每個元素，進行遞歸檢查當前目標金額下所有可能性
        for (int i = 0; i < coins.Length; i++)
        {
            //由於硬幣數值是最小到大順序排序的，如果某個硬幣幣值>目標金額，其後的硬幣幣值也一定>目標金額
            //而題目要求我們返回一個「剛好湊齊目標金額」（amount == 0）的方案，
            //因此當硬幣幣值>目標金額時，代表選擇該硬幣無法達成目標，可以直接中斷循環
            if(amount < coins[i]) { break; }
            //向下遞歸，得到該可能性下達到目標的步數
            int stepCnt = ClearCoinPathCounter(coins, amount - coins[i], memo);
            //確定返回當前層的步數不是-1（無法達到目標）以及小於當前最小值
            if(stepCnt >= 0 && stepCnt < minValue)
            {
                //步數 + 1
                minValue = stepCnt + 1;
            }
        }
        //記錄結果到存儲結果的數組裡
        memo[amount - 1] = minValue == int.MaxValue ? -1 : minValue;
        //返回當前層結果
        return memo[amount - 1];
    }
}

[LeetCode刷題筆記] 322 – Coin Change

題目描述：

一刷題解（Dynamic Programming）：

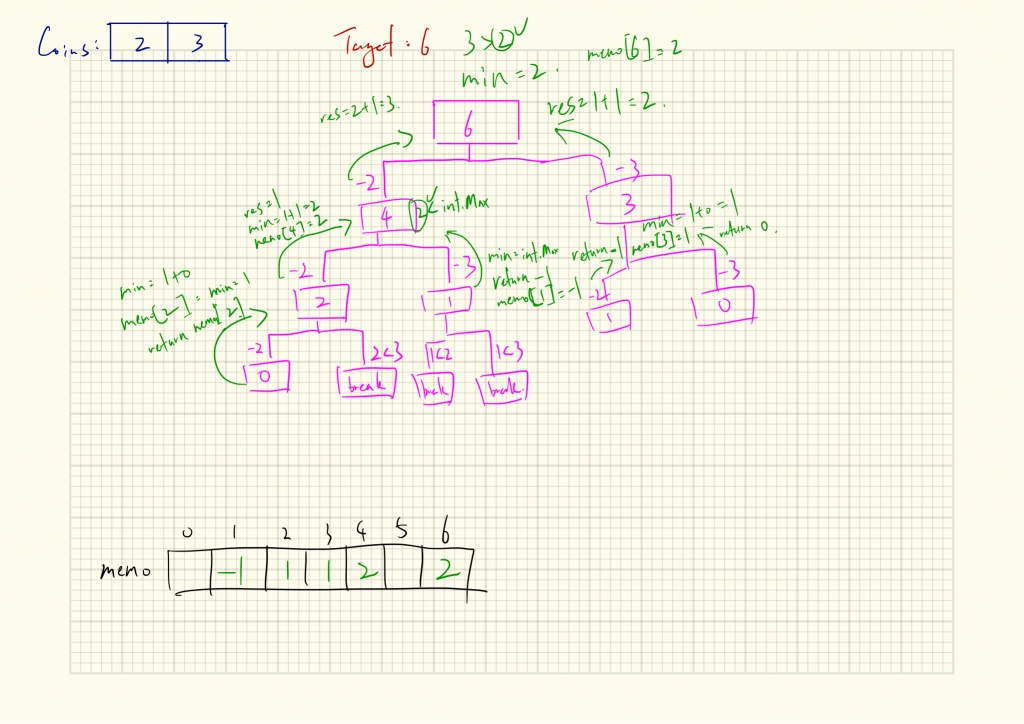
思路圖：