題目描述：
Determine if a 9 x 9 Sudoku board is valid. Only the filled cells need to be validated according to the following rules:
Each row must contain the digits
1-9without repetition.Each column must contain the digits
1-9without repetition.Each of the nine
3 x 3sub-boxes of the grid must contain the digits1-9without repetition.
Note:
A Sudoku board (partially filled) could be valid but is not necessarily solvable.
Example 1:
Input: board =
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
Output: true
Example 2:
Input: board =
[["8","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
Output: false
Explanation: Same as Example 1, except with the 5 in the top left corner being modified to 8. Since there are two 8's in the top left 3x3 sub-box, it is invalid.
Constraints:
board.length == 9board[i].length == 9board[i][j]is a digit or'.'.
一刷題解（HashSet）：
這題需要我們驗證一個9*9的數獨板子的當前數字配置是否符合數獨的規則。一個有效的數獨配置應該滿足：
- 每一行必須包含1-9所有數字，不能重複
- 每一列必須包含1-9所有數字，不能重複
- 每一個3*3共9格的子網格必須包含1-9所有數字，不能重複
這個板子可以只填充了部分格子，我們要做的就是驗證有數字的部分是否滿足這3個條件，而不需要去考慮這個9*9數獨是否能解。基於行、列和子網格都「不能有重複數字這個特點」，我們可以使用HashSet去驗證數字的是否出現重複。HashSet.Add會根據添加元素成功與否，返回一個bool，當出現重複數字並嘗試將其Add到HashSet裡時，由於HashSet不容許出現重複元素，因此它會返回一個false，我們就根據這個false得知這個當前數獨配置是失效的。
我們需要進行兩組驗證，一組是行/列的重複要素驗證、另一組是9個3*3子網格的重複要素驗證。
行/列的重複驗證比較簡單，只要使用兩層循環即可。外層循環(i)決定了當前循環的交點，交點是從左上角移動到右下角的，因此當i = 0時，交點位於左上角，i = 8時，交點位於右下角，每一次外層循環都會創建一個行HashSet和列HashSet，供內層循環檢查行列元素時使用；內層循環則是以當前交點為基礎，在行和列上的元素遍歷，並把值加到Hash裡。遍歷流程可參考下方示意圖：
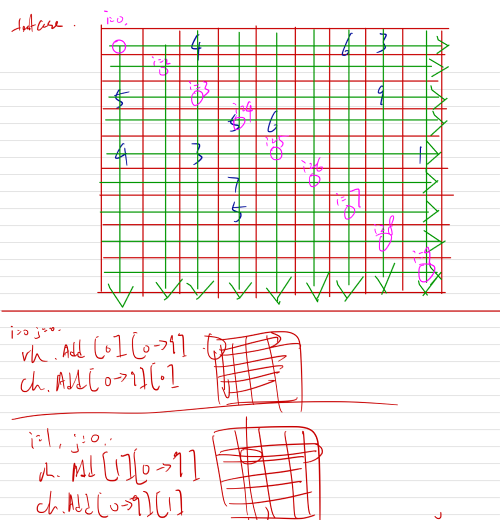
完成行列檢查後，就可以檢查子盒子的重複元素。整個數獨板的大小是9*9，每個子盒子的大小是3*3，也就是我們有3*3 = 9個子盒子。
我們共需要4個循環去完成子盒子的檢查，外面兩個循環是在整個數獨板上遍歷9個子盒子、為每個遍歷到的子盒子創建HashSet，根據當前遍歷到哪一行哪一列的子盒子去計算出該子盒子的行列起終點索引；裡面兩個循環則是根據外層遍歷得出的起終點索引進行遍歷，檢查子盒子範圍裡每個格子的元素，同樣通過HashSet.Add來檢查是否有重複元素。
當完成行列和子盒子的檢查後，仍然沒有發現重複元素，代表當前配置的數獨板是有效的。
public class Solution {
public bool IsValidSudoku(char[][] board) {
//Row/Col Check
for(int i = 0; i < board.Length; i++)
{
HashSet<int> rowHash = new HashSet<int>();
HashSet<int> colHash = new HashSet<int>();
for(int j = 0; j < board[0].Length; j++)
{
//將有一個row與col的交點從左上角往右下角移動，
//每次遍歷該交點的十字方向元素，當該交點到達右下角，每一行每一列都得到了確認
if(board[i][j] != '.' && !rowHash.Add(board[i][j])){ return false; } //Col Check
if(board[j][i] != '.' && !colHash.Add(board[j][i])){ return false; } //Row Check
}
}
//Box Check
for(int i = 0; i < 3; i++)
{
for(int j = 0; j < 3; j++)
{
//把整個3*3的九個方塊，每個方塊分一個HashSet
HashSet<int> boxHash = new HashSet<int>();
//方塊格子對應的x和y軸
int boxStartX = 3 * i; //0, 3, 6
int boxEndX = 3 * i + 3; //3, 6, 9
int boxStartY = 3 * j; //0, 3, 6
int boxEndY = 3 * j + 3; //3, 6, 9
for(int bx = boxStartX; bx < boxEndX; bx++)
{
for(int by = boxStartY; by < boxEndY; by++)
{
if(board[bx][by] != '.' && !boxHash.Add(board[bx][by])){ return false; }
}
}
}
}
}
}